설명
크루스칼 알고리즘은 프림 알고리즘과 함께 그래프에서 MST(Minimum Spanning Tree)를 찾을 때 사용 되는 알고리즘이다. 알고리즘을 전개하는 과정에서 소속집단의 검색과 합병기능이 필요한데, 이를 위해 유니온파인드에 대한 선행 학습이 필요하다.
유니온 파인드(Union Find)
설명 유니온 파인드는 집합의 표현을 빠르게 구현하는 알고리즘이다. 예를 들어보자. 사람 P1, P2, P3, P4가 있다. 각 사람은 자신의 소속집단 C1, C2, C3, C4에 가입되어 있다고 가정하자. 1. C3에 속한 P
seongmok.com
크루스칼 알고리즘은 사이클을 이루지 않고 크기가 작은 간선부터 탐색해 나아가는 방법을 사용한다. 이때, 사이클 생성 여부를 확인하기 위해 유니온 파인드를 사용한다.
다음과 같은 그래프가 있다.

위 그래프에 존재하는 모든 간선을 크기순으로 정렬한 뒤 사이클이 생기지 않는다면 선택한다.
현재 존재하는 간선 중 가장 크기가 작은 것은 정점3과 정점4를 잇는 간선이고, 이 간선을 선택해도 사이클이 생기지 않으므로 선택한다.
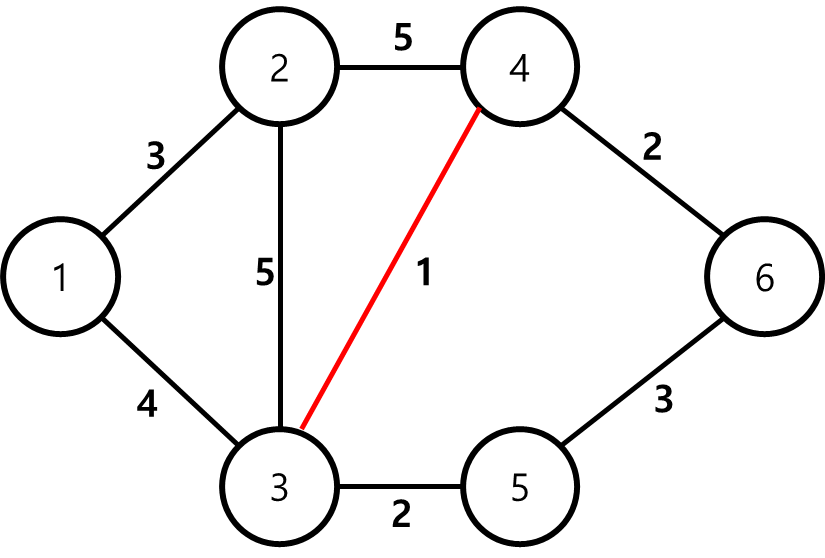
위 과정을 계속 반복하다보면 다음과 같은 상황을 마주친다. 이때, 선택되었던 간선들은 파란색으로 표시했다.
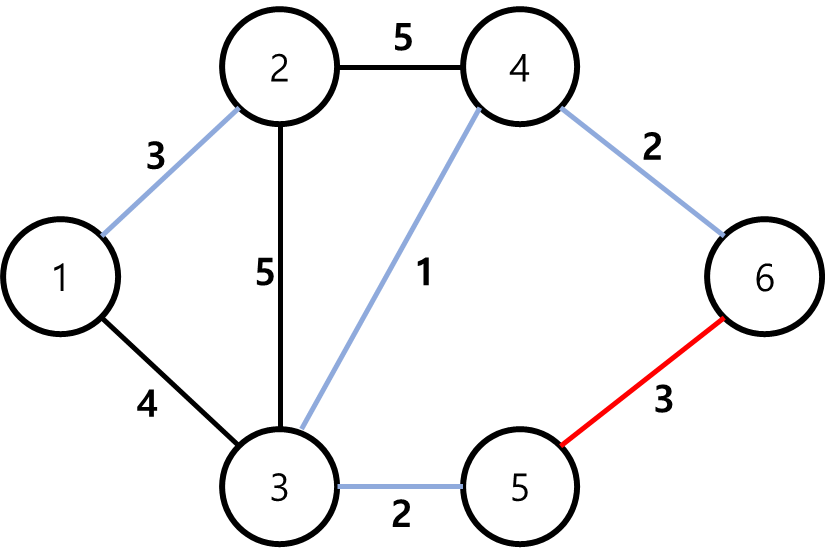
위 그림을 보면, 가중치의 크기순으로 선택하는 과정에서 현재 빨간색 간선을 보고있다.
그러나 정점5와 정점6을 잇는 순간, 정점3-정점4-정점6-정점5로 이루어진 사이클이 생기게 된다.
따라서 다음과 같은 과정을 이어나가게 된다.

이로써 MST를 찾아냈다. 위 과정으로 간선을 선택해 모든 정점으로 이루어진 Tree가 완성된다면, MST를 찾아낸 것이다. 또한, 이후 과정에서 마주치게 될 모든 간선들은 반드시 사이클을 이루게 만들기 때문에 선택되지 않는다.
따라서 구현의 과정에서 정점 V개에 대해 간선 V-1개가 이미 선택되었다면 더 이상 탐색을 하지 않는 방법을 통해 최적화를 진행할 수 있다.

구현
유니온 파인드에서 find, merge fucntion이 구현되어있어야 한다.
void kruskal(){
int num_edges = 0;
sort(edges.begin(), edges.end());
for(pair<int, int> edge : edges){
if(num_edges >= V-1) break;
if(find[edge.first] == find[edge.second]) continue;
merge(edge.first, edge.second);
is_selected[edge.first][edge.second] = is_selected[edge.second][edge.first] = true;
num_edges++;
}
}
시간복잡도
정점의 개수 V, 간선의 개수 E 일때, 각 단계의 유니온파인드 과정에서 소요되는 시간을 O(V)로 러프하게 잡아도 모든 간선을 정렬하는 과정에서 이미 O(ElogE)의 시간이 소요되기 때문에 전체 시간복잡도는 O(ElogE)로 표현될 수 있다.
또한, 만약 그래프가 Dense하다면, E = V^2 이므로, O(ElogV)로도 나타낼 수 있다.
추천문제
크루스칼 기본예제
1197번: 최소 스패닝 트리
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이
www.acmicpc.net
1922번: 네트워크 연결
이 경우에 1-3, 2-3, 3-4, 4-5, 4-6을 연결하면 주어진 output이 나오게 된다.
www.acmicpc.net
1647번: 도시 분할 계획
첫째 줄에 집의 개수 N, 길의 개수 M이 주어진다. N은 2이상 100,000이하인 정수이고, M은 1이상 1,000,000이하인 정수이다. 그 다음 줄부터 M줄에 걸쳐 길의 정보가 A B C 세 개의 정수로 주어지는데 A번
www.acmicpc.net
응용 심화문제
17472번: 다리 만들기 2
첫째 줄에 지도의 세로 크기 N과 가로 크기 M이 주어진다. 둘째 줄부터 N개의 줄에 지도의 정보가 주어진다. 각 줄은 M개의 수로 이루어져 있으며, 수는 0 또는 1이다. 0은 바다, 1은 땅을 의미한다.
www.acmicpc.net
2887번: 행성 터널
첫째 줄에 행성의 개수 N이 주어진다. (1 ≤ N ≤ 100,000) 다음 N개 줄에는 각 행성의 x, y, z좌표가 주어진다. 좌표는 -109보다 크거나 같고, 109보다 작거나 같은 정수이다. 한 위치에 행성이 두 개 이
www.acmicpc.net
유니온 파인드에 대한 선행이 되어있다면 어렵지 않게 이해할 수 있었다.
MST는 코딩테스트에서도 꽤나 자주 등장하는 만만한 알고리즘이기 때문에 학습해놓는 것이 좋다.
'코딩테스트 준비 > 알고리즘' 카테고리의 다른 글
| LIS(Longest Increasing Subsequence - 최장 증가 수열) 알고리즘 (1) (0) | 2021.09.03 |
|---|---|
| 임계경로(Critical Path) 알고리즘 (1) | 2021.09.02 |
| 플로이드-워셜(Floyd-Warshall) 알고리즘 (0) | 2021.08.30 |
| 다익스트라(Dijkstra) 알고리즘 (0) | 2021.08.29 |
| 유니온 파인드(Union Find) (0) | 2021.08.26 |




