임계경로(Critical Path)
! 본 글에서는 임계경로의 지나온 경로는 구하지 않고 임계경로의 길이만 구한다 !
그래프에서 임계경로란 어떤 시작지점으로부터 끝지점까지의 최장경로를 의미한다.
보통 그래프에서 경로의 길이를 구하면 최소경로를 찾는 것이 대부분이었을 것이다.
최장거리를 구한다는 것은 무슨 의미가 있을까?
다음과 같은 그래프가 있다고 가정하자.

위 그래프는 앞서 위상정렬(링크)에서 사용했던 그래프이다. 각 노드를 일이라고 표현해보자. 또한 빨간색 숫자는 각일을 할때 걸리는 시간이다.
해당 노드의 일을 끝내야 다음노드의 일을 끝낼 수 있다. 그렇다면 모든 일이 종료될때 까지의 최소시간은 무엇일까?
아무리 빠른 경로로 가서 마지막일을 끝내봤자 다른일이 끝나지 않았다면 의미가 없을 것이다.
이때 필요한 것이 임계경로(Critical Path) 알고리즘이다. 모든일을 끝내기위한 최소 시간은 시작노드로 부터 끝노드 까지의 최장경로의 길이를 구하면 될것이다.
최소시간을 구하기위해 최장경로를 구한다..는 말이 어렵지만 잘 생각해보면 이해가 될것이다.
설명
임계경로를 구하기 위해선 몇가지 조건이 필요하다.
1. 그래프에 cycle이 존재하면 안된다.
2. 그래프는 방향성을 가져야한다.
임계경로를 찾기위해 공부할 정도의 수준이라면 위 조건의 필요성을 굳이 설명하지 않겠다.

임계경로를 구하기위한 방법은 정말 많고 다양하지만 내가 생각하기에 가장 쉬운 방법으로 설명을 하겠다.
임계경로는 기본적으로 BFS알고리즘(링크)으로 구현이 가능하다.
과정은 간단하다.
BFS로 시작노드부터 그래프를 순환하며 더 큰 경로의 길이를 찾을때마다 업데이트하고 queue에 push하면 된다.
시작노드로부터 해당노드까지의 현재까지 찾은 최장거리를 dis[해당노드]로 표현하겠다.
또한 이 과정에서 indegree의 개수도 필요하다.
indegree란 자신에게 오는 edge의 수를 말한다. 위 예제에서 node4의 indegree는 2이다.
0. 시작 지점으로부터 각 노드까지의 최장거리는 초기에 0으로 세팅을 해놓는다. 또한 시작지점을 queue에 push한 채로 bfs탐색을 시작한다.
1. queue의 front를 현재노드로 설정한다.
2. q.pop()
3. 현재노드가 방문이 되었거나 현재 indegree 개수가 0이 아니라면 continue
4. 현재 노드로부터 연결된 노드들을 탐색하며 dis[현재노드]+다음노드로 갈 거리가 dis[다음노드]보다 크다면 dis값을 업데이트한다.
5. 4번에서의 다음노드를 push하고 다음노드의 indgree개수를 하나 줄인다.
6. queue가 empty상태일때 까지 2~5 반복
여기서 indegree가 감소한다는 의미는 방문한 edge를 제거한다는 의미이다.
과정을 그림으로 살펴보자.
초기 그래프는 다음과 같다.

노란색은 현재노드, 파란색은 큐에 있는 노드, 검은색은 방문이 끝난노드이다.
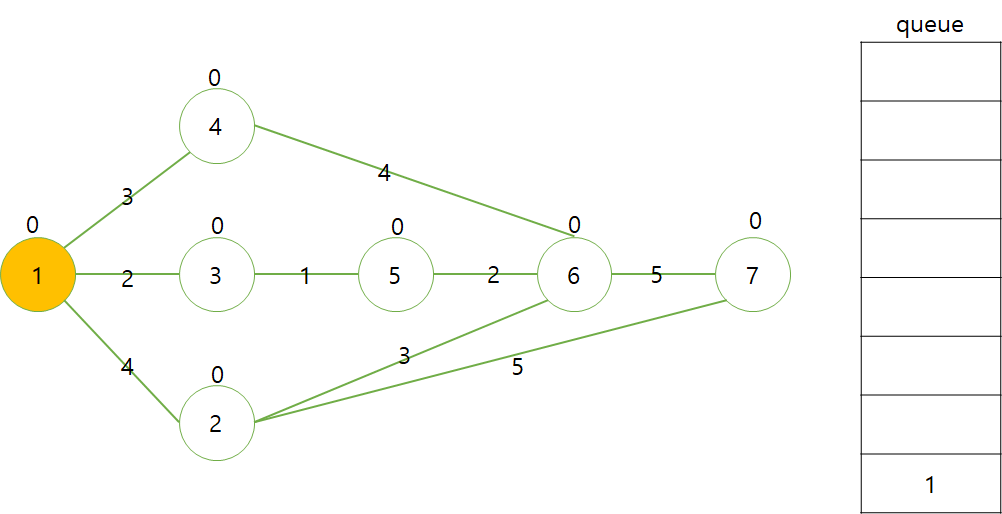










모든 과정이 끝나게 되면 dis[끝노드]의 값(12)이 해당 그래프 임계경로의 길이다.
구현
vector <vector <pair<int ,int>>> graph(n+1); // graph[현재노드] = vector<pair<다음노드, 거리>>
int bfs(vector <vector <pair<int ,int>>> &graph, int start,int end, int *dis, int *indeg){
bool visit[100001];
for(int i=1;i<=n;i++){
visit[i]=false;
}
queue <int> q;
q.push(start);
while(!q.empty()){
int curr = q.front();
q.pop();
if(visit[curr] || indeg[curr]!=0) continue;
visit[curr]=true;
for(int i=0;i<graph[curr].size();i++){
int des = graph[curr][i].first;
if(dis[des]<dis[curr]+graph[curr][i].second) {
dis[des] = dis[curr]+graph[curr][i].second;
}
q.push(des);
indeg[des]--;
}
}
return dis[end];
}
이 글에서는 임계경로의 길이만 구하는 방법을 알아봤다.
임계경로의 길이만을 필요로 하는 문제는 대표적으로 트리의 지름을 찾는 문제가 있다. (백준 1167 트리의 지름)
'코딩테스트 준비 > 알고리즘' 카테고리의 다른 글
| LIS(Longest Increasing Subsequence - 최장 증가 수열) 알고리즘 (2) (2) | 2021.09.04 |
|---|---|
| LIS(Longest Increasing Subsequence - 최장 증가 수열) 알고리즘 (1) (0) | 2021.09.03 |
| 크루스칼(Kruskal) 알고리즘 (0) | 2021.08.30 |
| 플로이드-워셜(Floyd-Warshall) 알고리즘 (0) | 2021.08.30 |
| 다익스트라(Dijkstra) 알고리즘 (0) | 2021.08.29 |



