다익스트라 (Dijkstra)
다익스트라는 어떤 그래프에서 특정노드에서 특정노드까지의 최단거리를 구할때 쓰는 알고리즘이다.
바로 예시를 들어보자.
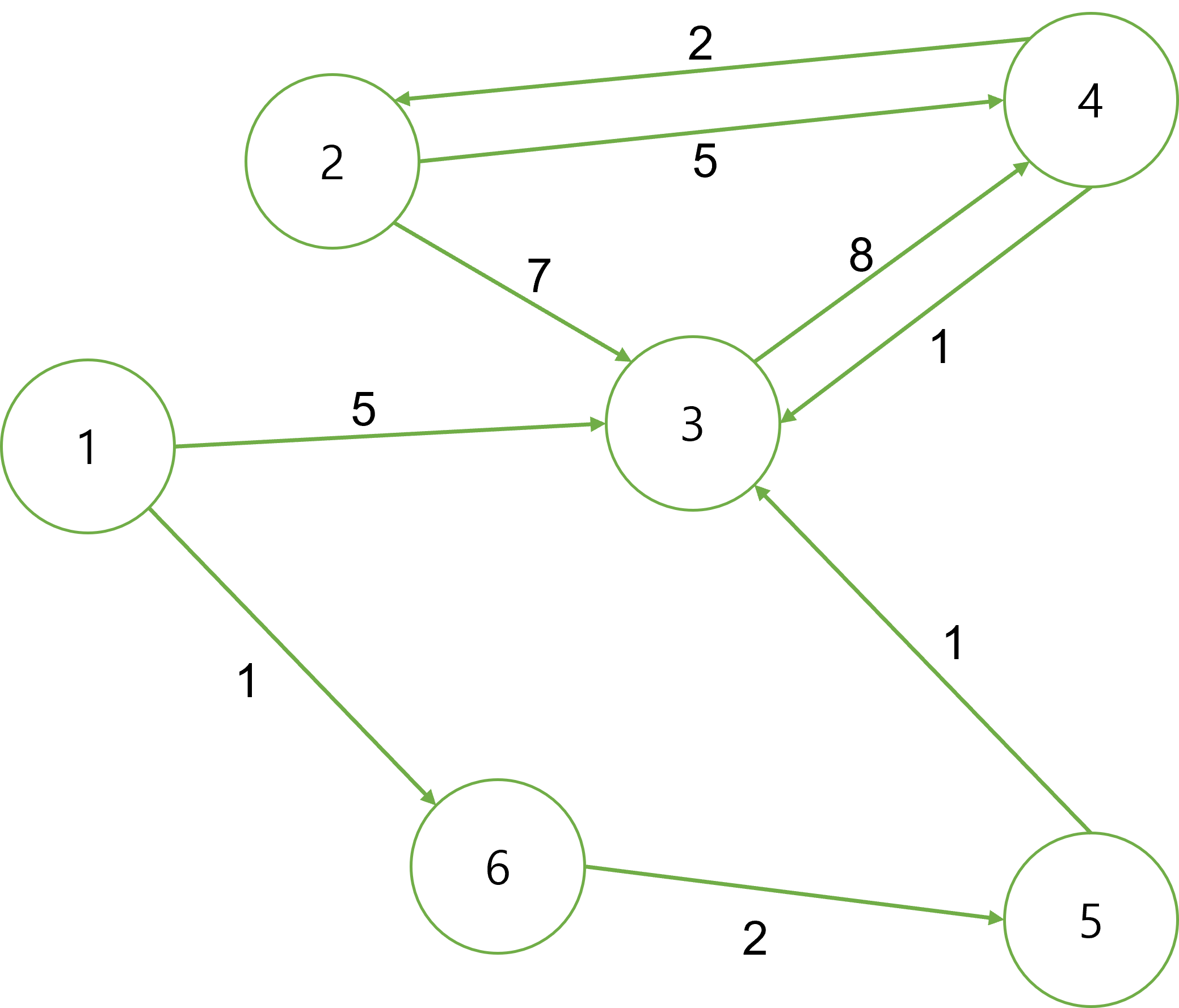
다음과 같은 그래프가 있다.
1번 노드에서 2번 노드로 가기위한 최소거리를 구할때 우리는 모든 엣지의 크기를 동시에 살피며 눈대중으로 찾을 것이다. 코딩을해서 찾는거보다 그냥 머리로찾는게 빠를거다.
그러나 노드의 개수가 많아지고 엣지의 개수가 많아지면 문제가 생긴다. 때문에 우리는 최단거리를 찾는 알고리즘을 통해 노드간의 최단거리를 찾아야 하는데 이에 대표적으로 사용되는 알고리즘이 바로 다익스트라이다.
설명

다익스트라는 BFS의 기본 틀에 우선순위 큐를 접목하여 구현할 수 있다.
BFS에 대한 설명은 여기(링크)에 있당!
1번 노드에서 각 노드로 가기위한 최소거리를 구하기 위해선 다음과 같은 절차를 밟는다.
다음 설명에서 말하는 큐는 우선순위 큐이다 (오름차순 정렬(가장 작은게 front)).
0. 1번노드를 큐에 넣고 1번노드를 제외한 모든노드에 대한 거리를 무한대로 설정해놓는다. (최소거리를 찾기 위함이므로)
1. 큐의 front를 현재노드로 설정한다. 현재노드로부터 연결되어있는 노드중 방문하지 않았으면 방문한다.
2. 현재 노드에 저장되어있는 거리 + 연결 되어있는 노드로의 거리가 연결 되어있는 노드에 저장되어있는 거리보다 작으면 업데이트 하고 큐에 push한다.
3. 연결되어있는 모든 노드를 돌면 현재노드를 방문표시로 하고 큐의 front(현재노드)를 pop한다.
4. 큐가 empty상태가 될때 까지 1~3을 반복한다.
위의 순서대로 진행하면 다음과 같다. (파란색은 현재노드, 노란색은 큐에 들어가있는 노드, 녹색은 방문이 끝난 노드)
빨간색은 1번노드부터 해당 노드까지의 현재 저장된 최소거리이다.
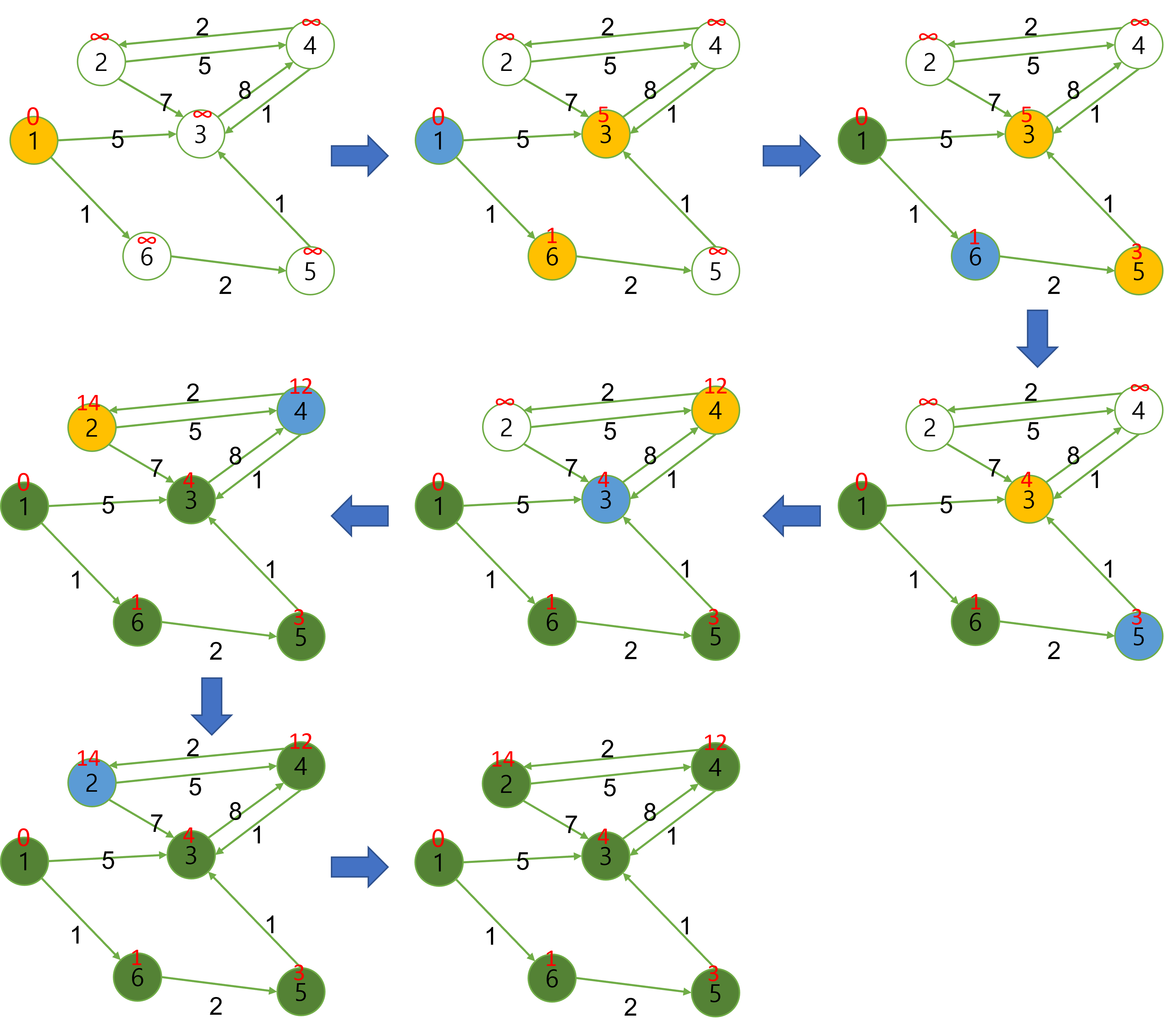
모든 방문이 끝난 후 어떤 노드에 저장되어있는 거리가 무한대라면 그 노드로 갈 수 있는 길이 없는것이다.
그렇다면 노드간의 거리가 음수일때는 어떨까?
위 과정을 정확이 이해한 사람이라면 어렵지않은 문제이다.
기본적으로 다익스트라는 음수인 엣지가 있는 경우에는 사용하지 않는다. (음수사이클이 있는 경우는 당연히 안됨)
Q. 어떤 엣지의 크기가 음수라면 그냥 그 음수의 절댓값만큼 모든 엣지에 더해서 가장 작은 엣지를 0으로 만들면 되지 않는가?
A. 안된다. 위의 경우에서 모든 엣지에 -5를 한 후 다익스트라를 적용시키면 1번노드에서 3번노드로 가는 최소거리는 -11이 된다. 그리고 처음에 빼줬던 5를 다시 더하면 -6이 되는데 이는 위의 과정으로 구한 결과와 다르다. 시작 노드부터 해당 노드까지 거치는 노드의 개수가 각각 다르므로 빼줬던 값들이 누적되어 정확한 결과가 나오지 않는다.
Q. 그렇다면 그냥 하면 되지 않는가?
A. 해도 된다. 그러나 거리가 누적되는 과정과 크기를 비교하는 과정에서 오류가 발생하기 쉽고, 음수사이클이 생길 가능성이 있기 때문에 지양하는것이 좋다.
구현
int dis[20001]; //시작노드로부터 해당인덱스의 노드까지의 최소거리 저장
bool visit[20001]; //방문여부
void dijkstra(vector <vector <int>> &graph, int start){
priority_queue <pair<int, int>, vector< pair<int, int>>, greater<pair<int, int>>> q;
q.push(make_pair(dis[curr],curr));
while(!q.empty()){
pair <int, int> temp = q.top();
int src_i = temp.second;
int src_w = temp.first;
q.pop();
if(visit[src_i]) continue;
visit[src_i] = true;
for(int i=0;i<graph[src_i].size();i++){
int des_i = graph[src_i][i].second;
int des_dis = graph[src_i][i].first;
if(visit[des_i]==false && (dis[des_i]==-1 || src_w+des_dis<dis[des_i])){
dis[des_i] = des_dis + src_w;
q.push(make_pair(dis[des_i],des_i));
}
}
}
}
만약 큐에 들어있던 노드의 거리저장값이 바뀌었다면 큐에서 해당노드를 지우고 다시 업데이트해서 push하는 것이 정확한 방법이지만, 시간을 매우 잡아먹고 효율적이지 않기 때문에 그냥 업데이트해서 새로 큐에 집어넣는다.
(우선순위 큐이고 방문체크를 따로 해주기때문에 상관없다.)
다익스트라는 최단거리 알고리즘중 가장 유명하고 기본적인 알고리즘이다.
다익스트라의 시간복잡도에 대해서 간단히 설명하자면 다음과 같다.
정점(노드)의 개수 : V
간선(엣지)의 개수 : E
우리는 지금 그래프의 정보를 2차원 배열이 아닌 이중벡터에 저장하고 있기 때문에 모든 정점과 간선들(그 정점에 연결된 정점들)에 접근할 때는 O(V+E)만큼의 시간이 소요된다.
또한 모든 정점 또는 간선들을 접근할때마다 업데이트(우선순위 큐 업데이트이므로 O(logV))가 된다고 생각하면 다익스트라의 시간복잡도는 O((V+E)logV)라고 할 수 있다.
즉, 다익스트라의 시간복잡도는 O(|E|*log|V|)이다.
'코딩테스트 준비 > 알고리즘' 카테고리의 다른 글
| 크루스칼(Kruskal) 알고리즘 (0) | 2021.08.30 |
|---|---|
| 플로이드-워셜(Floyd-Warshall) 알고리즘 (0) | 2021.08.30 |
| 유니온 파인드(Union Find) (0) | 2021.08.26 |
| 위상정렬 (Topological Sort) 알고리즘 (0) | 2021.08.26 |
| 펜윅트리(Fenwick Tree) 자료구조 (0) | 2021.08.26 |





