설명
탐색을 위해 사용되는 알고리즘이다.
이름에서 알 수 있듯이, 너비를 우선으로 탐색하기 때문에 단계적인 탐색을 위해 사용된다.
여기서 탐색이란, 대표적으로 그래프에서 정점 방문을 예로 들 수 있다. 또한, 어떤 작업의 처리에 대한 최소 단계 등을 요구하는 문제에서도 사용될 수 있다.
BFS를 구현하기 위해선 Queue가 필요하다. Queue는 선입선출으로 동작하기 때문에 가장 먼저 방문했던 단계의 이웃을 우선으로 탐색할 수 있다.
예제 보며 이해해보자.
다음과 같은 그래프가 있다. 정점1에서 시작해 그래프에 존재하는 모든 정점을 방문할 것이고, 한 정점에서 또 다른 정점은 간선을 통해 이동할 수 있다.

이때, 정점1에서 출발하여 각 정점 단계적으로 모두 방문하고 싶다.
단계적인 탐색이 필요하므로, BFS 알고리즘을 이용해 탐색할 수 있다.
현재 정점1에 위치하고 있고, 자신을 Queue에 PUSH한다.
또한, 이후의 과정에서 불필요한 재방문을 하지 않기 위해 방문체크 한다.

Queue의 Front를 POP한 후, 이 정점과 연결 되어있는 모든 정점을 Queue에 PUSH한 후 방문체크 한다.
이때, 어떤 정점을 먼저 PUSH할지에 대한 우선순위를 부여할 수도 있다.

Queue의 Front는 정점2가 되고, 이와 연결 된 정점 중 방문되지 않은 정점을 Queue에 PUSH하고 방문체크 한다.
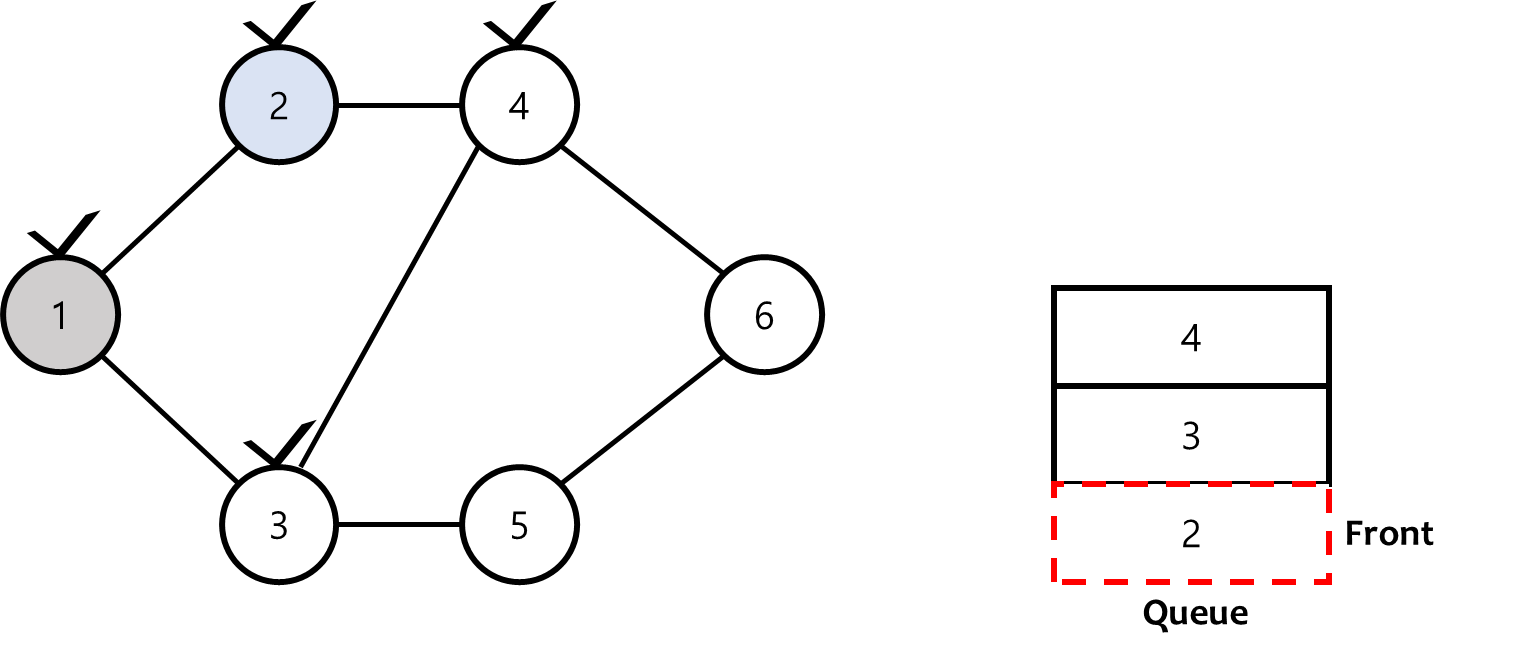
같은 방식으로 과정이 반복되면 다음과 같은 절차를 따른다.




이와 같이 단계적으로 탐색할 수 있다.
만약, 정점1에서 각 노드까지 소요되는 간선의 최소개수를 찾는 문제였다면 방문체크 대신 숫자를 이용하면 됐을 것이다.
위 예제에서는 그래프에서의 정점탐색을 위해 BFS를 사용했지만, 특정 조건을 만족하기 위한 연산의 최소 수 등의 예제에서도 충분히 활용될 수 있다.
구현
vector <vector<int>> graph;
bool visit[SIZE];
void bfs(int start){
memset(visit, false, sizeof(visit));
queue <int> q;
q.push(start);
visit[start] = true;
while(!q.empty()){
int src = q.front();
q.pop();
for(int dst : graph[src]) {
if(visit[dst]) continue;
visit[dst] = true;
q.push(dst);
}
}
}
시간복잡도
정점의 개수 V, 간선의 개수 E에 대해 각 정점과 간선을 모두 한번 씩 탐색하므로 O(V+E)의 시간복잡도로 표현할 수 있다.
추천문제
BFS 기본예제
2606번: 바이러스
첫째 줄에는 컴퓨터의 수가 주어진다. 컴퓨터의 수는 100 이하이고 각 컴퓨터에는 1번 부터 차례대로 번호가 매겨진다. 둘째 줄에는 네트워크 상에서 직접 연결되어 있는 컴퓨터 쌍의 수가 주어
www.acmicpc.net
7576번: 토마토
첫 줄에는 상자의 크기를 나타내는 두 정수 M,N이 주어진다. M은 상자의 가로 칸의 수, N은 상자의 세로 칸의 수를 나타낸다. 단, 2 ≤ M,N ≤ 1,000 이다. 둘째 줄부터는 하나의 상자에 저장된 토마토
www.acmicpc.net
응용된 심화버전 예제
4179번: 불!
입력의 첫째 줄에는 공백으로 구분된 두 정수 R과 C가 주어진다. 단, 1 ≤ R, C ≤ 1000 이다. R은 미로 행의 개수, C는 열의 개수이다. 다음 입력으로 R줄동안 각각의 미로 행이 주어진다. 각각의 문
www.acmicpc.net
2206번: 벽 부수고 이동하기
N×M의 행렬로 표현되는 맵이 있다. 맵에서 0은 이동할 수 있는 곳을 나타내고, 1은 이동할 수 없는 벽이 있는 곳을 나타낸다. 당신은 (1, 1)에서 (N, M)의 위치까지 이동하려 하는데, 이때 최단 경로
www.acmicpc.net
13460번: 구슬 탈출 2
첫 번째 줄에는 보드의 세로, 가로 크기를 의미하는 두 정수 N, M (3 ≤ N, M ≤ 10)이 주어진다. 다음 N개의 줄에 보드의 모양을 나타내는 길이 M의 문자열이 주어진다. 이 문자열은 '.', '#', 'O', 'R', 'B'
www.acmicpc.net
주로 코딩테스트에선 BFS를 응용하는 문제가 많이 출제된다.
0-1 BFS
최단거리 알고리즘을 이해한 후에 읽으신다면 목적을 더욱 분명하게 이해할 수 있습니다.
위 BFS에서는 각 단계의 탐색을 위해 Queue를 사용했다.
이는 각 현재 단계에서 방문하지 않은 이웃한 단계로 이동할 시 필요한 비용이 모두 동일했기 때문이다.

위 예제에서 만약 모든 간선을 방문할 때 필요한 비용이 1이라면 정점2까지 필요한 최소비용은 1이고, 정점6까지 필요한 최소비용은 3이다. 따라서 BFS를 이용해 탐색하면 답을 얻어낼 수 있다.
0-1 BFS 알고리즘은 방문하지 않은 이웃한 단계로의 이동에 필요한 비용이 0또는 1일때 사용할 수 있는 알고리즘이다.
보통 간선의 가중치가 모두 동일하지 않다면 특정 정점으로의 이동에 필요한 최소비용을 알고싶을 때 최단거리 알고리즘을 사용한다. 그러나 다익스트라, 벨만-포드 및 플로이드-워셜은 BFS보다 비싼 알고리즘이다. (더 높은 시간복잡도)
때문에 간선의 가중치가 0과 1로만 이루어져있다는 것이 보장된다면 비교적 시간복잡도가 낮은 BFS 알고리즘을 사용하자는 것이 이 알고리즘의 목적이다.
자료구조는 큐가 아닌 덱을 사용한다.
만약 이웃한 정점으로의 간선 가중치가 0이면 Front에 PUSH하고, 1이라면 Back에 PUSH한다. 이 과정을 통해 Front는 항상 최소 비용을 가지고 있음을 보장할 수 있다.
0-1 BFS를 학습하기 위해 좋은 예제가 있다.
13549번: 숨바꼭질 3
수빈이는 동생과 숨바꼭질을 하고 있다. 수빈이는 현재 점 N(0 ≤ N ≤ 100,000)에 있고, 동생은 점 K(0 ≤ K ≤ 100,000)에 있다. 수빈이는 걷거나 순간이동을 할 수 있다. 만약, 수빈이의 위치가 X일
www.acmicpc.net
BFS는 가장 많이 등장하는 알고리즘의 유형이다. 어느 상황에서든 응용할 수 있도록 자신의 기본 코드 틀을 갖춰놓는 것이 코딩테스트에서 중요하다.
'코딩테스트 준비 > 알고리즘' 카테고리의 다른 글
| 유니온 파인드(Union Find) (0) | 2021.08.26 |
|---|---|
| 위상정렬 (Topological Sort) 알고리즘 (0) | 2021.08.26 |
| 펜윅트리(Fenwick Tree) 자료구조 (0) | 2021.08.26 |
| 세그먼트 트리(Segment Tree) 자료구조 (0) | 2021.08.26 |
| DFS(Depth-First Search) (0) | 2021.08.26 |





